Time and Phase AlignmentΒΆ
This tutorial demonstrates how to use PyART to align waveforms in time and phase over a certain chosen time window.
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import seaborn as sns
# logging configuration, default INFO level
from PyART.logging_config import setup_logging
setup_logging()
# Set up Seaborn aesthetics
sns.set_context('talk')
sns.set_theme(font_scale=1.2)
sns.set_style('ticks')
# Update matplotlib rcParams
rcParams.update(
{
'text.usetex': False,
'font.family': 'stixgeneral',
'mathtext.fontset': 'stix',
'axes.grid': True,
'grid.linestyle': ':',
'grid.color': '#bbbbbb',
'axes.linewidth': 1,
}
)
from PyART.catalogs import sxs, rit
from PyART.utils import utils, wf_utils
We first download two waveforms from the SXS and RIT catalogs, respectively. These waveforms correspond to the same physical system: a BBH targeted to GW150914 (see Lovelace et. al.)
def align_wfs(wf1, wf2, time_window=[1000, 2500], ref=None, N_interp=20000):
"""
Align two waveforms based on the (2,2) mode.
Parameters
----------
wf1, wf2 : Waveform objects
The two waveforms to be aligned.
time_window : list, optional
Time window [start, end] (in M) over which to perform the alignment.
Default is [1000, 2500].
ref : float, optional
Reference time (in M) w.r.t. merger to align the waveforms. If provided, the alignment
will be done at this time instead of over a time window. Default is None.
N_interp : int, optional
Number of points for interpolation when aligning over a time window. Default is 20000.
Returns
-------
tau : float
Time shift (in M) to apply to wf1 to align with wf2.
dphi : float
Phase shift (in radians) to apply to wf1 to align with wf2.
"""
# align the (2,2) mode
h22_1 = wf1.hlm[(2,2)]
h22_2 = wf2.hlm[(2,2)]
# extract waveform 1
A_1, phi_1 = h22_1['A'], h22_1['p']
u_1 = wf1.u
imrg_1 = np.argmax(A_1)
u_1_mrg = u_1[imrg_1]
# extract waveform 2
A_2, phi_2 = h22_2['A'], h22_2['p']
u_2 = wf2.u
imrg_2 = np.argmax(A_2)
u_2_mrg = u_2[imrg_2]
# shift mergers to same point
u_1 = u_1 - u_1_mrg + u_2_mrg
tau = - u_1_mrg + u_2_mrg
if ref is not None:
# align at reference time w.r.t merger
t_mrg_1 = u_1[imrg_1]
t_mrg_2 = u_2[imrg_2]
i_ref_1 = utils.find_nearest(t_mrg_1+ref, u_1)
i_ref_2 = utils.find_nearest(t_mrg_2+ref, u_2)
dphi = phi_1[i_ref_1] - phi_2[i_ref_2]
dtau = u_2[i_ref_2] - u_1[i_ref_1]
else:
# common time array
u_new = np.linspace(max(u_1[0], u_2[0]), min(u_1[-1], u_2[-1]), N_interp)
win_start = u_2[utils.find_nearest(time_window[0], u_2)]
win_end = u_2[utils.find_nearest(time_window[1], u_2)]
dtau , dphi , _ = wf_utils.Align(u_new, win_end , win_end-win_start , u_1, phi_1, u_2, phi_2)
tau += dtau
return tau, dphi
# Waveforms
wf_sxs = sxs.Waveform_SXS(ID='0305', path='./', download=True, downloads=['hlm', 'metadata'], nu_rescale=False)
wf_rit = rit.Waveform_RIT(ID='0062', path='./', download=True, nu_rescale=False)
# pre-shift SXS to RIT merger time
wf_sxs._u -= wf_sxs.u[0]
wf_rit._u -= wf_rit.u[0]
t_mrg_rit, *_ = wf_rit.find_max()
t_mrg_sxs, *_ = wf_sxs.find_max()
wf_sxs._u += (t_mrg_rit - t_mrg_sxs)
# window for alignment
time_window = [500, 1000]
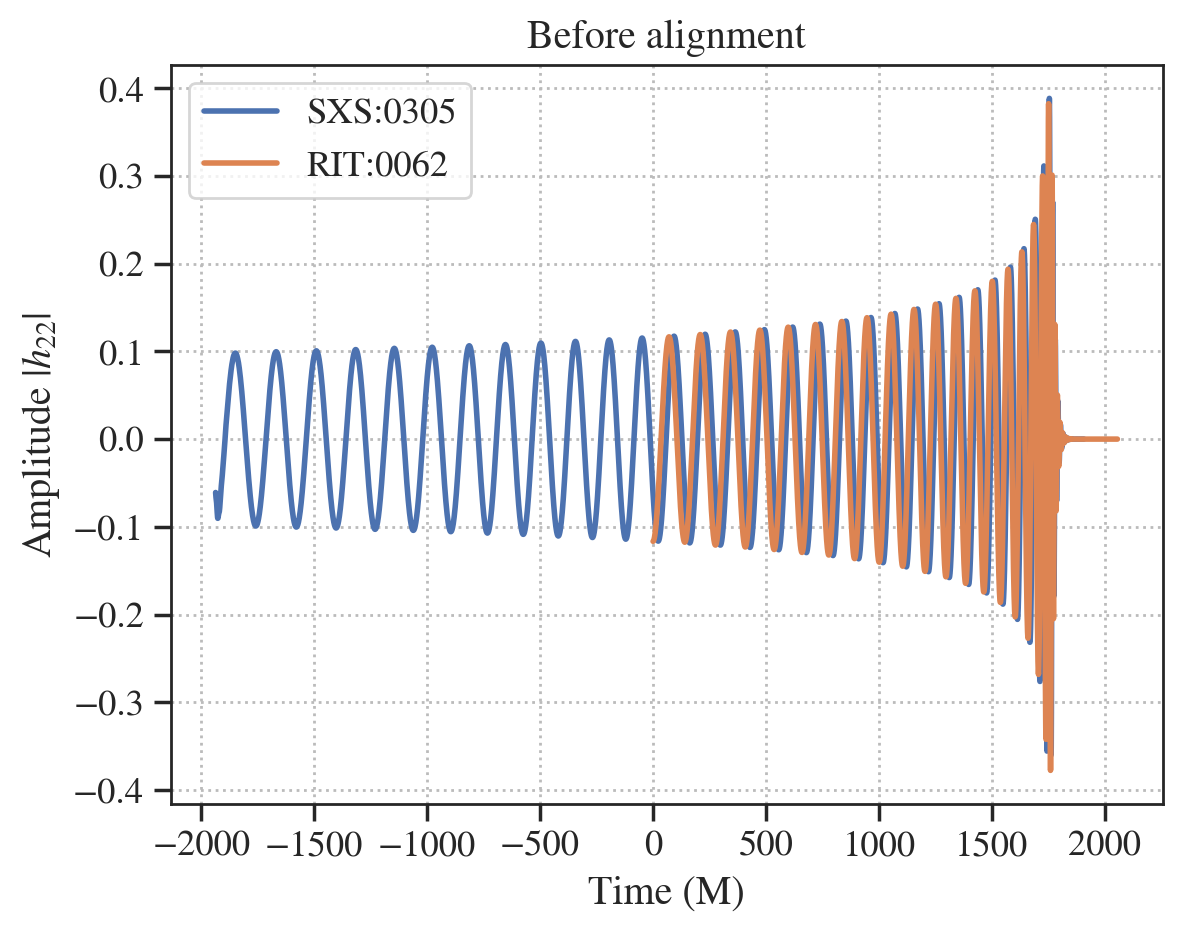
# plot the waveforms before alignment
fig, ax = plt.subplots()
ax.plot(wf_sxs.u, wf_sxs.hlm[(2,2)]['real'], label='SXS:0305', lw=2)
ax.plot(wf_rit.u, wf_rit.hlm[(2,2)]['real'], label='RIT:0062', lw=2)
ax.set_xlabel('Time (M)')
ax.set_ylabel(r'Amplitude $|h_{22}|$')
ax.legend()
ax.set_title('Before alignment')
plt.show()
# Align the two waveforms
tau, dphi = align_wfs(wf_rit, wf_sxs, time_window=time_window)
wf_rit._u += tau
print(f"Time shift (M): {tau:.2f}")
print(f"Phase shift (rad): {dphi:.2f}")
2025-12-10 00:54:27 The path ./SXS_BBH_0305 does not exist or contains no 'Lev*' directory.
2025-12-10 00:54:27 Downloading the simulation from the SXS catalog.
2025-12-10 00:54:27 Setting the download (cache) directory to ./
2025-12-10 00:54:36 Loaded SXS simulation SXS:BBH:0305.
2025-12-10 00:54:38 Saved hlm data.
2025-12-10 00:54:38 Saved metadata.
2025-12-10 00:54:39 The path ./RIT_BBH_0062 does not exist.
2025-12-10 00:54:39 Downloading the simulation from the RIT catalog.
2025-12-10 00:54:39 JSON file with RIT urls not found, fetching and parsing catalog webpage: https://ccrgpages.rit.edu/~RITCatalog/
2025-12-10 00:54:43 Created JSON file with RIT urls: /opt/hostedtoolcache/Python/3.11.14/x64/lib/python3.11/site-packages/PyART/catalogs/rit_urls.json
2025-12-10 00:54:43 --------------------------------------------------
2025-12-10 00:54:43 Downloading RIT:BBH:0062
2025-12-10 00:54:43 --------------------------------------------------
2025-12-10 00:54:43 wget-ing https://ccrgpages.rit.edu/~RITCatalog/Metadata/RIT:BBH:0062-n120-id3_Metadata.txt ...
2025-12-10 00:54:43 wget-ing https://ccrgpages.rit.edu/~RITCatalog/Data/ExtrapPsi4_RIT-BBH-0062-n120-id3.tar.gz ...
2025-12-10 00:54:44 Extracting ExtrapPsi4_RIT-BBH-0062-n120-id3.tar.gz ...
2025-12-10 00:54:44 wget-ing https://ccrgpages.rit.edu/~RITCatalog/Data/ExtrapStrain_RIT-BBH-0062-n120.h5 ...
2025-12-10 00:54:44 >> Elapsed time: 0.918 s
Time shift (M): 0.67
Phase shift (rad): -55.58
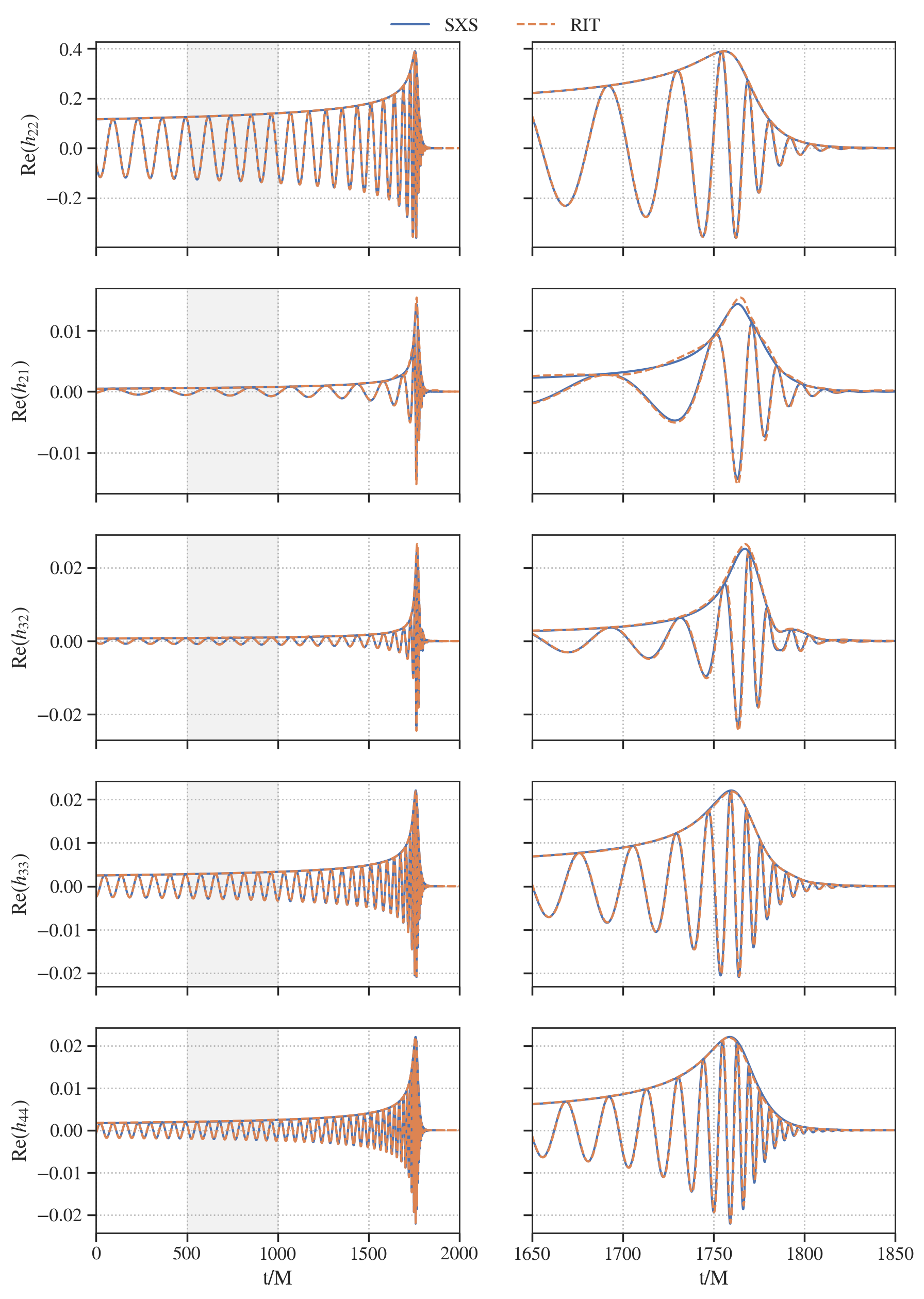
# propagate phase shift to all modes
modes = [(2,2), (2,1), (3,2), (3,3), (4,4)]
fig, ax = plt.subplots(len(modes), 2, figsize=(10, 3*len(modes)), sharex='col', sharey='row')
for j, (l, m) in enumerate(modes):
# note: the 2pi shift is sometimes required to get correct sign for odd-m modes
this_dphi = (dphi + 2*np.pi)*m / 2
h_lm = wf_rit.hlm[(l,m)]['z']
h_lm_shifted = h_lm * np.exp(1j * this_dphi)
# Plotting
for col in range(2):
ax[j, col].plot(wf_sxs.u, wf_sxs.hlm[(l,m)]['real'], label='SXS', color='C0', linestyle='-')
ax[j, col].plot(wf_rit.u, np.real(h_lm_shifted), label='RIT', color='C1', linestyle='--')
ax[j, col].plot(wf_sxs.u, wf_sxs.hlm[(l,m)]['A'],color='C0', linestyle='-')
ax[j, col].plot(wf_rit.u, np.abs(h_lm_shifted), color='C1', linestyle='--')
ax[j, 0].set_ylabel(r'Re$(h_{%d%d})$' % (l, m))
ax[j, 0].axvspan(time_window[0], time_window[1], color='gray', alpha=0.1)
ax[-1, 0].set_xlabel('t/M')
ax[-1, 0].set_xlim(0, 2000)
ax[-1, 1].set_xlabel('t/M')
ax[-1, 1].set_xlim(1650, 1850)
# legend on top of the figure
ax[0, 0].legend(loc='upper center', bbox_to_anchor=(1.1, 1.2), ncol=2, frameon=False)
plt.show()
