Vibin' and HOPINN

Thanksgiving came and went, and as an Italian living alone in the US there is not much to do during this time of the year.

Yes, of course, I could have worked on that one paper that I have been putting off for months now (it haunts me), or cleaned my apartment (it’s a mess), or called my family back home (I should do that more often). But honestly, none of the above sounded particularly appealing. No real work allowed during the Holidays, right? And while my apartment is chaotic, it is also functional, and one should never perturb the unstable equilibrium point! Finally, whenever I call home my mom tells me I look tired, I gained weight, I am getting wrinkles, or all of the above. She is right of course, but it still hurts.

So, instead, I decided to enjoy my alone time by doing something that always feels great: waste an afternoon “productively”, by attempting to learn something new, just for the fun of it. I spun the wheel of fun-topics-that-I-have-been-curious-about-for-a-while, and it landed on Physics Informed Neural Networks (or PINNs, for the cool kids).

Physics Informed Neural Networks – what’s that?

What are PINNs, you ask? While I am certainly not an expert (I wouldn’t be making this post otherwise), my understanding is the following:

PINNs are a type of neural network that uses the physical laws governing a system to inform and constrain the learning process. Such laws usually come in the form of differential equations (ODEs or PDEs), which the network learns to satisfy while also fitting any available data.

Pretty cool huh?! They already have found applications in many fields of physics, but I sort of stumbled upon them while scrolling through the arXiv a while ago.

So yeah, I decided to give it a try. And as a physicist, whenever I want to learn something new, I like to have a project in mind to apply it to. In my day-to-day research, I very often have to deal with systems of ODEs, be it when computing the stellar structure of neutron stars, or when evaluating the orbital evolution of binary systems under the effect of gravitational wave emission. But those problems are complicated, and I wanted to start simple. So, I went back to the most common, most basic system that any respectable scientist should know all about: the 1D harmonic oscillator.

What’s in a name?

Before I get into the details of my little Holiday project, a quick note on the title of this post. Recently, I have been encountering on Twitter the term “vibe coding”. To the best of my knowledge, it refers to the practice of “writing” code by giving prompts to large language models (like ChatGPT, Gemini, etc.), while supervising and guiding them along the way. Personally, I have a love-hate relationship with LLMs: I can’t deny they are useful (I use them to edit my paper drafts to fix grammar and spelling), but I greatly worry about their impact on the environment and on society at large. So I figured that this would be a good opportunity to put them to the test: were my “vibe coding” attempts to fail, I could convince myself that I am not obsolete (yet); were they to succeed, I could save some time and learn something new. Win-win?

HOPINN: how it went down

TLDR: I wanted to code a PINN to solve the coupled Hamiltonian ODEs of a 1D harmonic oscillator:

\begin{equation} \frac{dx}{dt} = v \end{equation}

\begin{equation} \frac{dv}{dt} = - \omega^2 x \end{equation}

where \(x\) is the position of the oscillator, \(v\) its velocity, and \(\omega\) its frequency, given some initial conditions \(x(t_0) = x_0, v(t_0) = v_0\). The solution is simple and well known (left as an exercise to the reader!), so it is very easy to check if the PINN is working correctly.

Two notes:

1. I think that this is not the most efficient formulation of the problem for a PINN: it would probably be easier for the network to try and learn the second order ODE \begin{equation} \frac{d^2 x}{dt^2} + \omega^2 x = 0 \end{equation} instead of the coupled first order system. But I wanted to try something a bit closer to the real problems I usually deal with.
2. In principle, there are two way to go at this problem: either have the network learn to solve the ODEs for fixed \(\omega\), or have it learn to solve the ODEs for any \(\omega\) (i.e., have \(\omega\) as an input parameter). The latter is obviously more powerful, but also more challenging because the network has to learn a family of solutions instead of just one. This post will most likely focus only on the fixed-omega case, but I might try to extend it in a future post. Or not, who knows!

Having said all of the above, I proceeded to prompt ChatGPT (the free version, of course) with the following:

ChatGPT, implement for me a physics informed neural network in pytorch to solve the coupled hamiltonian ODEs of a 1D harmonic oscillator:
dx/dt = v
dv/dt = - omega**2 * x
The PINN should take as input the time t, and output the position x and velocity v of the oscillator at that time.
The loss function should include a term to enforce the ODEs, as well as a term to fit any initial conditions provided.
Please provide the full code, including the training loop and an example of how to use the PINN to solve the ODEs.

As you can imagine, the first few attempts were… less than stellar. The code was bugged and/or incomplete. It did, however, provide a pretty decent starting point. After a few iterations of prompting, debugging and refining, I finally got an implementation that would run without errors. Hooray! Here comes the catch though: I quickly realized that running and working correctly, when dealing with neural networks, are two very different things. The model, while it did train, we not learning to solve the ODEs. It reminded me a little bit of my own attempts at doing pull-ups at the gym. Anyways, ChatGPT was not much help at this point: it would just repeat that I should train for more epochs, or adjust the learning rate, or change the architecture, mentioning that “experimentation is key when working with neural networks”. Thanks, I guess?

After a few hours of tinkering, I finally managed to get a model that would go from the initial conditions to a reasonable solution. I ended up using a simple architecture with four hidden layers and tanh activation. The loss function was a combination of the ODE residuals evaluated at 100 collocation points, and the “initial condition” loss evaluated at five points (one of which outside of the collocation range), the latter weighted more heavily than the former. I trained the model for 7000 epochs using the Adam optimizer with a learning rate scheduler that would halve the learning rate every 1500 epochs or so. For more details, you can check out the full code on my GitHub.

Success?

Here is the result of the trained model compared to the analytical solution (dashed black) for omega=1 after 7000 epochs of training. The darker a line, the larger the training epoch. I’m also showing the region where I fixed the collocation points (shaded gray) and the initial conditions (red dots).

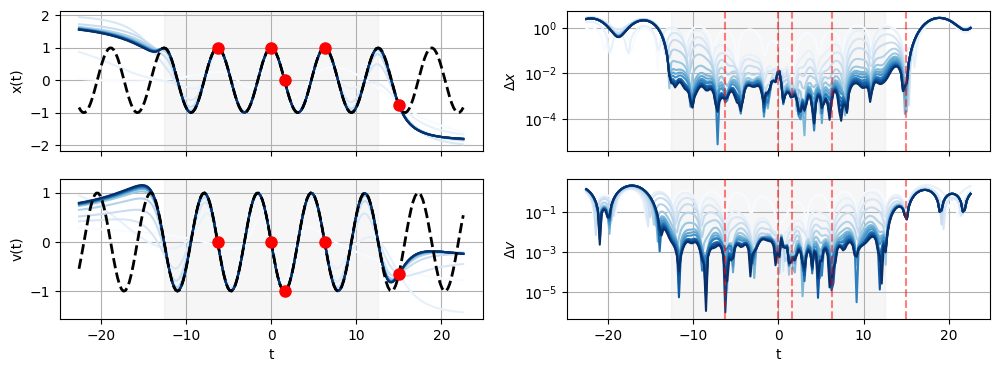
Pretty neat, I suppose, for an afternoon of work. The models works reasonably well within the training range, and seems to be able to extrapolate a little bit. I am pretty sure that with more tinkering one could impose additional constraints (e.g. periodicity) to further improve the performance.

As for the vibe coding aspect of this project, the experience was mixed. ChatGPT was definitely helpful in getting a feeling for the overall structure of the code that I needed to write, but I had to take care of most of the details myself. And as one says, the devil is in the details.

Anyway, next step will be to extend this to accept omega as an input parameter, so that the network can learn a family of solutions. Stay tuned for part 2 of this Holiday project! (assuming I don’t get bored and abandon it halfway through, that is).